
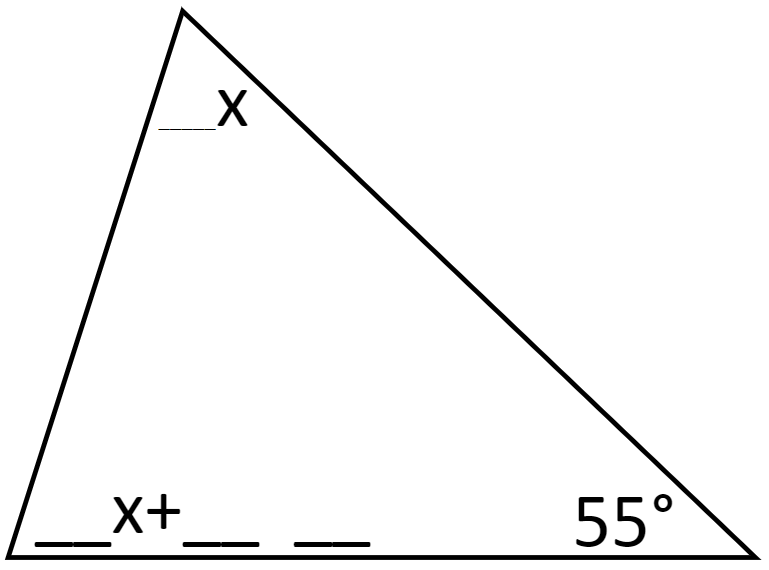
Then construct the bisector of ∠ABC by following the procedure outlined below: Step 1: With the compass point at B, draw an arc that intersects BA and BC. Label the intersection points D and E respectively. Step 2: With the compass point at D and then at E, draw two arcs with the same radius that intersect in the interior of ∠ABC. Write a proof that ray BF bisects ∠ABC.Įxploring Constructions with Geometer’s Sketchpad G.G.20a Construct an equilateral triangle with sides of length b and justify your work.Įxploring Constructions with Geometer’s Sketchpad G.RP.3e, G.RP.5c, G.CM.5e Construct an angle of 300 and justify your construction.Įxploring Constructions with Geometer’s Sketchpad G.R.1b, G.R.3a, G.R.5a, G.G.30a Using a dynamic geometry system draw ΔABC similar to the one below. Drag a vertex and make a conjecture about the sum of the interior angles of a triangle. Extend this investigation by overlaying a line on side AC. Measure the exterior angle at C and the sum of the interior angles at A and B. Justify your conjectures.Įxploring Constructions with Geometer’s Sketchpad G.G.43bĮxploring Constructions with Geometer’s SketchpadĮxploring Constructions with Geometer’s Sketchpad G.PS.2d, G.CM.1c, G.G.21a Using dynamic geometry software, locate the circumcenter, incenter, orthocenter, and centroid of a given triangle. #GSP5 CONSTRUCTING A PERPENDICULAR BISECTOR ANSWERS HOW TO#.Q3 Do you think a regular heptagon (seven sides) would tessellate? Explain. Q2 Which of the regular polygons you tried will tessellate and which won’t? Why? Answer on a separate sheet.

Repeat the investigation with squares, regular pentagons, regular hexagons, and regular octagons. Why do equilateral triangles work? (Hint: It has to do with their angles.) 6. You can tile the plane with them without gaps or overlapping. Q1 So far, you’ve demonstrated that equilateral triangles can tessellate. Keep attaching triangles to edges of existing triangles until you have triangles completely surrounding at least two points.
Drag several points on the triangles to make sure they’re really attached. Use the custom tool again, this time clicking in the opposite direction, to construct a second equilateral triangle attached to the first. Pay attention to the direction in which the triangle is created as you use the tool. On a blank page, or in a blank sketch, use a custom tool to construct an equilateral triangle. Open the sketch Islamic_Tessellations.gsp if it is not already opened. Such custom tools come with the sketch below, but you may want to create them yourself. Each custom tool must create its figure from the endpoints of one side of the polygon-not from the center. You’ll need custom tools for creating equilateral triangles, squares, regular pentagons, regular hexagons, and regular octagons.

Are there other shapes that would make good tiles? In this investigation, you’ll discover which regular polygons tessellate. This kind of tiling is sometimes called a tessellation. Squares make good tiles because they can cover a surface without any gaps or overlapping. Tessellating with Regular Polygons Name(s): You’ve probably seen a floor tiled with square tiles. You must always start and end your dragging with the cursor positioned on an existing point. If your triangles don’t stay attached, undo until the second triangle goes away, then try again.
Click twice in the sketch to use the tool. Click on the Custom tools icon (the bottom tool in the Toolbox) and choose the desired tool from the menu that appears.


 0 kommentar(er)
0 kommentar(er)
